Introduction
Visualization has a major impact on the understanding and exploration
of complex mathematical phenomena. As in other sciences, images are used in mathematics as
helpful illustrations accompanying textual descriptions, as a communication medium to
exchange ideas with other cooperating researchers, and to explain deep mathematical
results in a comprehensive way to non-experts, just to mention only a few applications.
The process of visualization is a synonym for a broader process than
the production of images or video animations. Prior the generation of images, abstract
mathematical concepts must be translated into discrete descriptions which are numerical
data structures to hold the mathematical information. For example, a smooth surface must
be discretized in a set of triangles, and algorithms must be translated from their smooth
counterparts acting on smooth geometries to discrete geometries.
In general these conversions are delicate tasks. For example a Riemann
surface may have different smooth descriptions requiring non-obvious discrete structures
such as triangulated piecewise linear surfaces with specific discrete properties.
Continuous Riemann surfaces are identified under conformal maps, and so one would like to
perform a similar identification on the corresponding discrete objects. It is of central
importance in mathematical visualization to have discrete equivalents of smooth concepts,
and discrete algorithms on discrete surfaces which perform the same operation as their
counterparts on smooth concepts.
The process of defining useful discrete data structures, finding good
discretization algorithms, and deriving methods operating on discrete geometries belongs
to the same category of mathematical tasks which have been so important for smooth
geometries. Good visualization and numerics rely on perfect discrete definitions which are
the basis to assign, measure and transform mathematical properties of discrete geometries.
Numerical mathematics has gone a long way in discretizing function spaces but, for
example, the understanding of the intrinsic mathematical properties of discrete geometric
shapes still leads to challenging questions.
 It is important
to distinguish between the process of visualizing precomputed numerical data and, in other
sciences, of experimentally measured data, and the process of doing numerical experiments
and simulations. The first process is an analytic process trying to understand large sets
of numbers by the means of finding good visual representations. This includes hiding and
emphasizing of data as well as the feature extraction of detail information. Many
visualization tools operate in a post-processing step by evaluating large data sets and
generating new smaller sets with feature information. For example, one of the current
major problems is the visualization of turbulent 3d flows. Because of its complexity the
flow might be unaccessible to a direct visual representation but the path of moving
vortices may be computed and easier to display. Here the correct definition of vortices in
a discrete flow is an essential prerequisite before starting the development of a tracing
algorithm. The second process of doing numerical experiments and simulations is a
constructive and repetitive process where an experiment is analysized during runtime and
information obtained to steer parameters and interact with the numerical process. Here
visualization is used to obtain insight into the behavior of a running algorithm rather
than into geometric dataset.
It is important
to distinguish between the process of visualizing precomputed numerical data and, in other
sciences, of experimentally measured data, and the process of doing numerical experiments
and simulations. The first process is an analytic process trying to understand large sets
of numbers by the means of finding good visual representations. This includes hiding and
emphasizing of data as well as the feature extraction of detail information. Many
visualization tools operate in a post-processing step by evaluating large data sets and
generating new smaller sets with feature information. For example, one of the current
major problems is the visualization of turbulent 3d flows. Because of its complexity the
flow might be unaccessible to a direct visual representation but the path of moving
vortices may be computed and easier to display. Here the correct definition of vortices in
a discrete flow is an essential prerequisite before starting the development of a tracing
algorithm. The second process of doing numerical experiments and simulations is a
constructive and repetitive process where an experiment is analysized during runtime and
information obtained to steer parameters and interact with the numerical process. Here
visualization is used to obtain insight into the behavior of a running algorithm rather
than into geometric dataset.
Over the past years, visualization has proven to be a successful tool
for mathematicians in the investigation of difficult mathematical problems which seem to
be unaccessible by standard mathematical tools. It has proven its potential by
substantially contributing to the solution of hard mathematical problems.
 Mathematicians often have a concrete imagination of abstracts shapes
even in higher dimensional spaces, and especially geometers have a deeply visually related
thinking. Images are very helpful during their research, they give insight into unknown
phenomena and suggest directions for further investigations. Nevertheless there is a
remarkable contrast between the visual thinking, and the occurrence of pictures in
research publications and inner-mathematical talks. Often images are extremely rare, for
example, books on differential geometry, a mathematical subject with one of the largest
fundus of easily visualizable complex geometric shapes, contain only a handful figures
with most simplest shapes. The lectures on differential geometry of Luigi Bianchi is a
comprehensive and very influential book on surface theory, whose German translation was
published in 1910, and the classic book on Riemannian Geometry by Gromoll, Klingenberg,
and Meyer from 1969, which was the book for a generation of geometers, both books contain
no single image of a surface or a geometric shape. Similar examples up to modern days
could be listed.
Mathematicians often have a concrete imagination of abstracts shapes
even in higher dimensional spaces, and especially geometers have a deeply visually related
thinking. Images are very helpful during their research, they give insight into unknown
phenomena and suggest directions for further investigations. Nevertheless there is a
remarkable contrast between the visual thinking, and the occurrence of pictures in
research publications and inner-mathematical talks. Often images are extremely rare, for
example, books on differential geometry, a mathematical subject with one of the largest
fundus of easily visualizable complex geometric shapes, contain only a handful figures
with most simplest shapes. The lectures on differential geometry of Luigi Bianchi is a
comprehensive and very influential book on surface theory, whose German translation was
published in 1910, and the classic book on Riemannian Geometry by Gromoll, Klingenberg,
and Meyer from 1969, which was the book for a generation of geometers, both books contain
no single image of a surface or a geometric shape. Similar examples up to modern days
could be listed.
In some sense images have the character of an experiment: they suggest
a truth or result but usually do not have the power of a proof. An image can illustrate a
mathematical proof but an experiment or image implicitly requests a formal proof of its
suggested result. Nevertheless, important experimental results exist which have not been
rigorously proven, but they direct theoretical investigations and often give final hints.
Experiments have been performed in the whole history of mathematics but only since 1991
there exists a publication media, the journal of Experimental Mathematics.
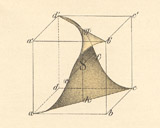 In contrast to a wide-spread opinion, mathematical history contains a
rich set of visual examples. Archimedes was drawing figures into the sand when being
bothered by the Romans during the capturing of Syracuse. Euclidean geometry, nowadays
referred to as 'elementary geometry', is one of prominent examples where all kinds of
drawings always played a central role in the communication and publication of results.
Famous non-trivial examples are the copper plate engravings of Hermann Amandus Schwarz
shown in the figure besides [10]. He discovered new
minimal surfaces which solved long-standing questions in geometry and analysis on the
existence of solutions to elliptic boundary value problems. Although his proof was of
theoretical nature he found it worthwhile to invest a lot of energy to include visual
images of the new surfaces into his research publications. This is remarkable if compared
to the much less effort one needs for the generation of computer images today.
In contrast to a wide-spread opinion, mathematical history contains a
rich set of visual examples. Archimedes was drawing figures into the sand when being
bothered by the Romans during the capturing of Syracuse. Euclidean geometry, nowadays
referred to as 'elementary geometry', is one of prominent examples where all kinds of
drawings always played a central role in the communication and publication of results.
Famous non-trivial examples are the copper plate engravings of Hermann Amandus Schwarz
shown in the figure besides [10]. He discovered new
minimal surfaces which solved long-standing questions in geometry and analysis on the
existence of solutions to elliptic boundary value problems. Although his proof was of
theoretical nature he found it worthwhile to invest a lot of energy to include visual
images of the new surfaces into his research publications. This is remarkable if compared
to the much less effort one needs for the generation of computer images today.
 One
of the most thorough approaches in mathematics to use physical models and experimental
instruments in education and research is the famous collection of mathematical models in
Göttingen. This model collection already had a long history when Hermann Amandus Schwarz
and Felix Klein overtook the direction of the collection. Especially under the direction
of Klein the collection was systematically modernized and completed for the education in
geometry and geodesy. This collection was considered so important that Klein exhibited the
models on the occasion of the World's Columbian Exposition 1893 in Chicago [2]. The models were produced among others by the publisher
Martin Schilling in Halle a.S., see his catalog of mathematical models [9]. The price of approximately $250 per model was
relatively, and therefore, the large size of the collection of more than 500 plaster
models is even more impressive. The collection can still be seen in the mathematical
department in Göttingen, and a description including photos of many models is given in
Fischer [4]. An example is the plaster model of the Kuen
surface in the figure besides.
One
of the most thorough approaches in mathematics to use physical models and experimental
instruments in education and research is the famous collection of mathematical models in
Göttingen. This model collection already had a long history when Hermann Amandus Schwarz
and Felix Klein overtook the direction of the collection. Especially under the direction
of Klein the collection was systematically modernized and completed for the education in
geometry and geodesy. This collection was considered so important that Klein exhibited the
models on the occasion of the World's Columbian Exposition 1893 in Chicago [2]. The models were produced among others by the publisher
Martin Schilling in Halle a.S., see his catalog of mathematical models [9]. The price of approximately $250 per model was
relatively, and therefore, the large size of the collection of more than 500 plaster
models is even more impressive. The collection can still be seen in the mathematical
department in Göttingen, and a description including photos of many models is given in
Fischer [4]. An example is the plaster model of the Kuen
surface in the figure besides.
 Shown here is a modern model of the Chen-Gackstatter-Karcher-Thayer
minimal surface produced in stereo lithography technique from digital data. The production
of models slowed down and finally stopped in the beginning 30s. Following Fischer, the
reasons were not purely economical nature but also the appearance of more general and
abstract view points in mathematics. It was the time when the books of van der Waerden
with only simple illustrations, and of Nicolas Bourbaki with a complete ignorance of
images appeared.
Shown here is a modern model of the Chen-Gackstatter-Karcher-Thayer
minimal surface produced in stereo lithography technique from digital data. The production
of models slowed down and finally stopped in the beginning 30s. Following Fischer, the
reasons were not purely economical nature but also the appearance of more general and
abstract view points in mathematics. It was the time when the books of van der Waerden
with only simple illustrations, and of Nicolas Bourbaki with a complete ignorance of
images appeared.
 It seems that minimal surfaces have been among those geometric shapes
which often urged mathematicians and physicists to produce images. In the sequel to
Schwarz and the experiments of Joseph Antoine Ferdinand Plateau, it was Richard Courant,
Johannes C.C. Nitsche, and Alan H. Schoen who experimented with physical soap films and
even produced real models for permanent display and for easier communication. Among the
first breakthroughs of mathematical visualization was the proof of embeddedness of another
minimal surface.
It seems that minimal surfaces have been among those geometric shapes
which often urged mathematicians and physicists to produce images. In the sequel to
Schwarz and the experiments of Joseph Antoine Ferdinand Plateau, it was Richard Courant,
Johannes C.C. Nitsche, and Alan H. Schoen who experimented with physical soap films and
even produced real models for permanent display and for easier communication. Among the
first breakthroughs of mathematical visualization was the proof of embeddedness of another
minimal surface.  Celsoe Costa discovered the
mathematical formulae of a genus 1 minimal surface which was a candidate to solve a
200-year long question: whether there exists a third embedded and complete minimal
surfaces with finite total curvature beside the trivial examples, the flat plane and the
rotational symmetric catenoid. David Hoffman and William Meeks developed computer programs
to visualize Costa's surfaces and watch surface properties which they could later
successfully prove after having enough insight into the complex shape of the surface, see
figures besides and [7].
Celsoe Costa discovered the
mathematical formulae of a genus 1 minimal surface which was a candidate to solve a
200-year long question: whether there exists a third embedded and complete minimal
surfaces with finite total curvature beside the trivial examples, the flat plane and the
rotational symmetric catenoid. David Hoffman and William Meeks developed computer programs
to visualize Costa's surfaces and watch surface properties which they could later
successfully prove after having enough insight into the complex shape of the surface, see
figures besides and [7].
 It is important
to distinguish between the process of visualizing precomputed numerical data and, in other
sciences, of experimentally measured data, and the process of doing numerical experiments
and simulations. The first process is an analytic process trying to understand large sets
of numbers by the means of finding good visual representations. This includes hiding and
emphasizing of data as well as the feature extraction of detail information. Many
visualization tools operate in a post-processing step by evaluating large data sets and
generating new smaller sets with feature information. For example, one of the current
major problems is the visualization of turbulent 3d flows. Because of its complexity the
flow might be unaccessible to a direct visual representation but the path of moving
vortices may be computed and easier to display. Here the correct definition of vortices in
a discrete flow is an essential prerequisite before starting the development of a tracing
algorithm. The second process of doing numerical experiments and simulations is a
constructive and repetitive process where an experiment is analysized during runtime and
information obtained to steer parameters and interact with the numerical process. Here
visualization is used to obtain insight into the behavior of a running algorithm rather
than into geometric dataset.
It is important
to distinguish between the process of visualizing precomputed numerical data and, in other
sciences, of experimentally measured data, and the process of doing numerical experiments
and simulations. The first process is an analytic process trying to understand large sets
of numbers by the means of finding good visual representations. This includes hiding and
emphasizing of data as well as the feature extraction of detail information. Many
visualization tools operate in a post-processing step by evaluating large data sets and
generating new smaller sets with feature information. For example, one of the current
major problems is the visualization of turbulent 3d flows. Because of its complexity the
flow might be unaccessible to a direct visual representation but the path of moving
vortices may be computed and easier to display. Here the correct definition of vortices in
a discrete flow is an essential prerequisite before starting the development of a tracing
algorithm. The second process of doing numerical experiments and simulations is a
constructive and repetitive process where an experiment is analysized during runtime and
information obtained to steer parameters and interact with the numerical process. Here
visualization is used to obtain insight into the behavior of a running algorithm rather
than into geometric dataset. 




